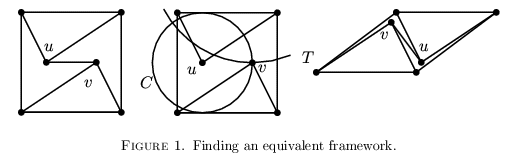
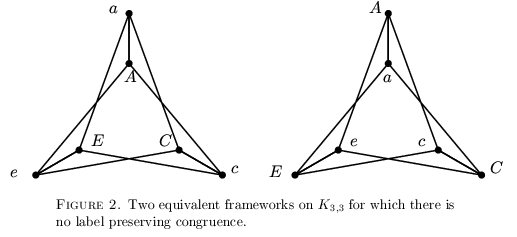
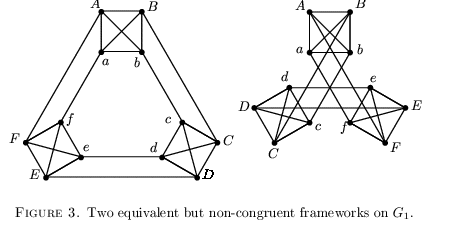
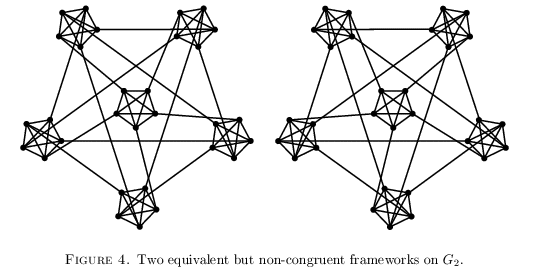
Author: Bill Jackson , Brigitte Servatius , and Herman Servatius

Reference: Journal of Graph Theory, Volume 54, Issue 2, 154--166, February 2007.

Selected Figures:

Abstract: Laman's characterization of minimally rigid 2-dimensional generic frameworks gives a matroid structure on the edge set of the underlying graph, as was first pointed out and exploited by L.\ Lov\'asz and Y.\ Yemini. Global rigidity has only recently been characterized by a combination of two results due to T. Jord\'an and the first named author, and R. Connelly, respectively. We use these characterizations to investigate how graph theoretic properties such as transitivity, connectivity and regularity influence (2-dimensional generic) rigidity and global rigidity and apply some of these results to reveal rigidity properties of random graphs. In particular, we characterize the globally rigid vertex transitive graphs, and show that a random $d$-regular graph is asymptotically almost surely globally rigid for all $d \geq 4$.